搜索到
50
篇与
人工智能炼丹师
的结果
-
-
购房规划 1. 确定预算 购房成本计算(首付+各项税费) 2. 确定购房地理位置(地铁&学校) 深圳控规图查询 安居客-深圳2022楼盘 深圳地铁规划图 3. 选择小区，对比物业 深圳市房地产信息平台: 查小区各项信息(包括具体单元销售情况等) 物业服务评价信息查询 4. 现场实地看房 现场看房注意事项 5. 选楼层 好楼层 1/3-2/3的楼层: 公认的黄金楼层，无遮挡，采光好，通风好，视野好，蚊虫少，噪音少 8，9，10 楼层: 楼层不高不低，采光和通风效果虽然没有高楼层效果好，但是也并不差; 火灾时更易逃生 差楼层 顶层/一楼/二楼：不仅受外界干扰较多，房屋的采光条件也较差 腰线层上下两层: 腰线的上下两层就是腰线层，其中下一层采光会被遮挡，腰线部分的积水也会渗透到室内 设备层上下两层：有供暖、供电或供水枢纽设备的那层。因为设备的噪音、机械振动等会给居住环境带来负面影响
-
Pandas学习笔记 DataFrame 常用方法 Groupby的用法 Apply的用法 axis参数可用于指定按行处理还是按列处理 遍历DataFrame方法 DataFrame访问行列 # 根据row index name索引 df.loc[INDEX_NAME] # 根据column name 索引 df[COLUMN_NAME] DataFrame和Dict的相互转换 Dict to DataFrame: pandas.DataFrame.from_dict Series 常用方法 一些不常用的操作 # 对未命名column进行重命名 data.rename(columns={'Unnamed: 0':'new column name'}, inplace=True) 参考链接 Pandas 官方教程 Pandas 官方API Pandas教程 | 超好用的Groupby用法详解 Pandas|常见用法整理 10min快速入门
-
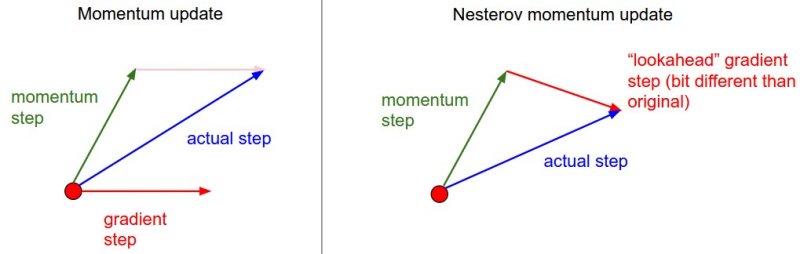
一阶梯度优化方法小结 1. 前言 梯度下降法的基本原理是，通过对目标函数做泰勒展开，当变量的运动方向与梯度方向相同，目标函数值增长最快；负梯度方向，目标函数值减小最快。这里主要讨论将目标函数做一阶泰勒展开，也就是一阶梯度优化方法。利用二阶泰勒展开,即牛顿法需要计算Hessian矩阵的逆，计算量大，在深度学习中并不常用。BGD(Batch Gradient Decent)利用整个训练集计算梯度，优化速度慢，需要一次将所有数据加载进内存不适用于在线学习，因此，在神经网络的优化中常采用mini-batch SGD(Stochastic Gradient Descent)进行优化。SGD主要存在以下两个问题： 难以确定学习率，并且不同的参数需要不同大小的学习。SGD比BGD收敛更快，但在最优解附近可能调整过大，导致在最优点附近震荡，因此基于SGD的算法，随着迭代的进行，不断减小学习率来解决这个问题。例如Caffe中有poly,inv,step等策略来调整学习率 鞍点(各个方向，梯度为0)的存在使得基于梯度的优化方法，难以逃离鞍点 2. 主要内容 SGD+Momentum NAG AdaGrad RMSProp AdaDelta Adam 这里主要以尽可能简单的语言总结各个算法的内容，具体细节参考文末链接
-
Developing new layers in caffe caffe官方的层更新的速度还是比较慢，有时不得不自己实现新的层。本文以实现L2 normalize为例(详细代码，可以查看CaffeLayers)，简单记录下实现的过程。 实现新的层，主要步骤如下: 实现xx_layer.hpp 实现xx_layer.cpp 实现xx_layer.cu 修改caffe.proto(可选) 实现test_xx_layer.cpp(可选,推荐完成) 在实现的过程中顺便对C++的语法进行简要的复习。 normalize_layer.hpp 我们需要定义NormalizeLayer这个类，这个类需要从抽象类Layer 中继承。声明需要改写的虚函数。LayerSetUp() 、type() 、 限制该层的输入bottom和top个数 和 Forward_cpu() 、 Forward_gpu() Backward_cpu() 、Backward_gpu() 等。 NormalizeLayer() 构造函数NormalizeLayer()用Layerparameter& param作为形参，并调用父类的构造函数实现。 explicit NormalizeLayer(const Layerparameter ¶m) :Layer<Dtype>(param){} 注: explicit 可以避免构造函数被调用造成隐式转换，用explicit声明的构造函数只能用于直接初始化 LayerSetUp() 完成网络建立时，从prototxt中读取Layer的参数，可通过this->layerparam 访问该层的参数并对类的成员变量进行初始化并为网络的权重参数分配存储。 NormalizeLayer中没有参数，所以这一步可以省略掉。 virtual void LayerSetUp(const vector<Blob<Dtype>*>& bottom, const vector<Blob<Dtype>*>&top); type() type() 函数是一个返回层的层的种类的inline函数，形式如 virtual inline const char* type() const {return "Normalize";} Reshape() Reshape()与LayerSetUp的功能类似，但是LayerSetUp() 只在网络初始化时被调用，而reshape是在每次前向计算前，根据Bottom的大小动态计算Top的大小并分配存储(只要与Bottom大小相关的都要重新分配存储)。在此处，需要重新分配存储的是top和成员变量, 通过调用Blob的Reshape函数即可。 virtual void Reshape(const vector<Blob<Dtype>*>& bottom, const vector<Blob<Dtype>*>& top); Blobs数目相关 virtual inline int ExactNumBottomBlobs() const {return 1;} virtual inline int ExactNumTopBlobs() const {return 1;} 前向后项传播(CPU&GPU) virtual void Forward_cpu(const vector<Blob<Dtype>*>& bottom, const vector<Blob<Dtype>*>& top); virtual void Forward_gpu(const vector<Blob<Dtype>*>& bottom, const vector<Blob<Dtype>*>& top); virtual void Backward_cpu(const vector<Blob<Dtype>*>& top, const vector<bool>& propagate_down, const vector<Blob<Dtype>*>& bottom); virtual void Backward_gpu(const vector<Blob<Dtype>*>& top, const vector<bool>& propagate_down, const vector<Blob<Dtype>*>& bottom); 类成员变量的声明 //保留前向的中间变量，可以减少反向传播中相同表达式的计算量 //squared_: bottom的平方(Elememt-wise) //norm_: 由样本特征的L2范数构成的向量(size: num) //sum_multiplier_: GPU实现辅助变量 Blob<Dtype> sum_multiplier_, norm_, squared_; normalize_layer.cpp 实现normalize_layer.hpp中相关函数的定义， 在normalize_layer.cpp 中，我们需要对前向Forward_cpu，后向Backward_cpu，Reshape进行实现。 Reshape template <typename Dtype> void NormalizeLayer<Dtype>::Reshape(const vector<Blob<Dtype>*>& bottom, const vector<Blob<Dtype>*>& top){ top[0]->Reshape(bottom[0]->num(), bottom[0]->channels(), bottom[0]->height(), bottom[0]->width()); squared_.Reshape(bottom[0]->num(), bottom[0]->channels(), bottom[0]->height(), bottom[0]->width()); } Forward_cpu 前向操作比较简单即 y=x/||x|| template <typename Dtype> void NormalizeLayer<Dtype>::Forward_cpu(const vector<Blob<Dtype>*>& bottom, const vector<Blob<Dtype>*>& top){ const Dtype* bottom_data = bottom[0]->cpu_data(); Dtype* top_data = top[0]->mutable_cpu_data(); Dtype* squared_data = squared_.mutable_cpu_data(); int n = bottom[0]->num(); int d = bottom[0]->count() / n; caffe_sqr<Dtype>(n*d, bottom_data, squared_data); for (int i=0; i<n; ++i) { Dtype normsqr = caffe_cpu_asum<Dtype>(d, squared_data+i*d)+(Dtype)1e-10; caffe_cpu_scale<Dtype>(d, pow(normsqr, -0.5), bottom_data+i*d, top_data+i*d); } } Backward_cpu 这里先简单介绍下NormalizeLayer的反向求导。 $E=f(y_{1},y_{2},...y_{n})$ $E=f(y_{1}(x_{1},s(x_{1},x_{2},...,x_{i})),y_{2}(x_{2},s(x_{1},x_{2},...,x_{i},...x_{n})),y_{i}(x_{i},s(x_{1},x_{2},...,x_{i},...x_{n}))$ 其中$s =\left \| x\right \| = \sqrt{x_{1}^{2}+x_{2}^{2}+...+x_{n}^{2}},y_{i}=\frac{x_{i}}{s}$,n表示向量的维度 $\frac{\partial E}{\partial x_{i}} =\frac{\partial E}{\partial y_{i}}*\frac{\partial y_{i}}{\partial x_{i}}+\sum_{j=1}^{n} \frac{\partial E}{\partial y_{j}}*\frac{\partial y_{j}}{\partial s}*\frac{\partial s}{\partial x_{i}} =\frac{\partial E}{\partial y_{i}}*(\frac{1}{s}+\sum\_{j=1}^{n}(-\frac{x_{j}}{s^2})*(\frac{x_{j}}{s}))=\frac{\partial E}{\partial y_{i}}*\frac{1}{s}(1-\sum_{j=1}^{n}y_{j}^{2})=\frac{\partial E}{\partial y_{i}}*\frac{1}{s}(1-y \cdot y)$ void NormalizeLayer<Dtype>::Backward_cpu(const vector<Blob<Dtype>*>& top, const vector<bool>& propagate_down,const vector<Blob<Dtype>*>& bottom){ const Dtype* top_diff = top[0]->cpu_diff(); const Dtype* top_data = top[0]->cpu_data(); const Dtype* bottom_data = bottom[0]->cpu_data(); Dtype* bottom_diff = bottom[0]->mutable_cpu_diff(); int n = top[0]->num(); int d = top[0]->count() / n; for (int i=0; i<n; ++i) { Dtype a = caffe_cpu_dot(d, top_data+i*d, top_diff+i*d); caffe_cpu_scale(d, a, top_data+i*d, bottom_diff+i*d); caffe_sub(d, top_diff+i*d, bottom_diff+i*d, bottom_diff+i*d); a = caffe_cpu_dot(d, bottom_data+i*d, bottom_data+i*d); caffe_cpu_scale(d, Dtype(pow(a, -0.5)), bottom_diff+i*d, bottom_diff+i*d); } } 实例化模板类 #ifdef CPU_ONLY STUB_GPU(NormalizeLayer); #endif INSTANTIATE_CLASS(NormalizeLayer); REGISTER_LAYER_CLASS(Normalize); STUB_GPU 定义GPU的前向后向操作 INSTANTIATE_CLASS 实例化模板类 REGISTER_LAYER_CLASS 完成类的注册(工厂模式) normalize_layer.cu caffe中将大部分数学操作都实现了GPU和CPU两种版本，例如，caffe_cpu_dot 和 caffe_gpu_dot,所以一般的层的GPU实现只需要把CPU实现的函数改成对应的GPU版本就可以。 修改caffe.proto(可选) 由于Normalize该层没有需要设置的参数，所以caffe.proto并不需要修改. 实现test_normalize_layer.cpp 为了验证自己编写层的正确性，我们通过在test中测试层的前向和反向操作。caffe中运用Google C++ Testing Framework 来进行测试。关于gtest，可以参考gtest in caffe 编写完测试文件，重新编译，进行测试 $ make $ make test $ make runtest GTEST_FILTER='NormalizeLayerTest/*' Note：最后一条命令行不要漏了/* ! Reference caffe wiki--Development caffe wiki--Simple Example: Sin Layer math_functions help test_gradient_check_util
-
Caffe之Cuda C caffe中能够很方便地切换CPU或者GPU模式，但是如果我们想要develop 新的层，则需要写cpp和cu文件，相比之下theano比caffe的扩展方便地多。首次读Caffe的代码，简单记录学习下cu文件如何实现。 CUDA C CUDA C最简单的形式就是C语言而已，如果不涉及GPU的操作，当然这样也还是能够被NVIDIA的编译器NVCC所编译。 __global__ void kernel(void){} CUDA 中 __global__ 表明该函数在device(GPU)设备上运行，并且由host(CPU)调用。例如一个加法程序 __global__ void add(int* a, int* b, int*c) { *c = *a + *b; } int main(void) { int a,b,c; int *gpu_ptr_a,gpu_ptr_b,gpu_ptr_c; int size = sizeof(int); cudaMalloc((void**)&gpu_ptr_a,size); cudaMalloc((void**)&gpu_ptr_b,size); cudaMalloc((void**)&gpu_ptr_c,size); a = 2; b = 7; cudaMemcpy(gpu_ptr_a,&a,size,cudaMemcpyHostToDevice); cudaMemcpy(gpu_ptr_b,&b,size,cudaMemcpyHostToDevice); add<<<1,1>>>(gpu_ptr_a,gpu_ptr_b,gpu_ptr_c); cudaMemcpy(&c,gpu_ptr_c,size,cudaMemcpyDeviceToHost); cudaFree(gpu_ptr_a); cudaFree(gpu_ptr_b); cudaFree(gpu_ptr_c); return 0; } 内存管理 CUDA对device(GPU )的内存管理主要通过cudaMalloc()、cudaFree()、cudaMemcpy() 进行管理。另外，从上述代码我们可以看到，add() 函数的调用比较奇怪相对于C语言来说，需要用add<<<M，N>>> 这种形式表明这是一个从host(CPU)代码调用device的代码，并且括号中的数值表明，M个block，每个block有 N个线程, 所以这个函数总共有M*N个线程。 CUDA 并行操作 CUDA中用来实现并行操作的有block 和thread 两个模块。 block在代码中用blockIdx.x 指示。blockIdx.x为cuda中内建(build-in)的变量，它表明正在执行状态下的block的index。Cuda允许使用多维的索引，.x 为常用的一维索引。一个block可以切分成不同的threads。 thread 在代码中用 threadIdx.x表示线程的标号。thread是block的进一步划分，thread好处在于并行的block难以进行通信和同步(Communciate and Synchronize )，thread通过Shared Memory 在线程之间进行同步，在CUDA C用关键字__shared__ 表示。 #define N 512 __global__ void dot(int *a,int *b, int *c) { __shared__ int temp[N]; temp[threadIdx.x] = a[threadIdx.x] * b[threadIdx.x]; __syncthreads(); if(0 == threadIdx.x) { int sum = 0; for(int i=0; i<N; i++) { sum += temp[i] ; } *c = sum; } } 上述代码实现了向量点积的过程。 涉及到多线程操作和内存共享的问题，必须要考虑线程之间的同步。__syncthreads() 实现的就是这个目的，只有当所有的线程运行到了__syncthreads() 处(即共享的temp[N]已经运算完成)线程才能继续向下执行，否者temp[N] 还没写完就去读，sum得到的结果就未知了。 sigmoid_layer.cu 简析 cu文件的组成: host(CPU)调用的函数Forward_gpu()和Backward_gpu() 在device(GPU)上计算的核函数(由CPU中的函数调用) 实例化函数模板,包括Forward_gpu()和Backward_gpu() 下面以sigmoid_layer的CUDA实现进行简要分析。 template <typename Dtype> __global__ void SigmoidForward(const int n, const Dtype* in, Dtype* out) { CUDA_KERNEL_LOOP(index, n) { out[index] = 1. / (1. + exp(-in[index])); } } 上面是sigmoid的前向传播函数的核函数，这里CUDA_KERNEL_LOOP其实是定义在在device_alternate.hpp 的宏，CUDA_KERNEL_LOOP的详细解释可以参考这篇问答 #define CUDA_KERNEL_LOOP(i, n) \ for (int i = blockIdx.x * blockDim.x + threadIdx.x; \ i < (n); \ i += blockDim.x * gridDim.x) 但是caffe中与此处 的解释不太相同。caffe中固定每个block中线程的个数, 即然后根据元素的个数动态分配block的数目，定义如下 // CUDA: use 512 threads per block const int CAFFE_CUDA_NUM_THREADS = 512; // CUDA: number of blocks for threads. inline int CAFFE_GET_BLOCKS(const int N) { return (N + CAFFE_CUDA_NUM_THREADS - 1) / CAFFE_CUDA_NUM_THREADS; } 所以利用CAFFE_GET_BLOCKS 方法，线程的个数始终大于或等于元素个数N，故不存在一个线程 for循环处理多个元素。在CUDA_KERNEL_LOOP 中，只有在线程的个数小于元素个数N的情况下for循环才起效。 Forward_gpu() 、 Backward_gpu() 调用核函数实现就不展开介绍了。 最后cu文件还需要对Forward_gpu()和Backward_gpu() 进行显示实例化(instantiation)。 INSTANTIATE_LAYER_GPU_FUNCS(SigmoidLayer); 上述代码是Caffe中定义的一个宏，具体展开如下 #define INSTANTIATE_LAYER_GPU_FORWARD(classname) \ template void classname<float>::Forward_gpu( \ const std::vector<Blob<float>*>& bottom, \ const std::vector<Blob<float>*>& top); \ template void classname<double>::Forward_gpu( \ const std::vector<Blob<double>*>& bottom, \ const std::vector<Blob<double>*>& top); #define INSTANTIATE_LAYER_GPU_BACKWARD(classname) \ template void classname<float>::Backward_gpu( \ const std::vector<Blob<float>*>& top, \ const std::vector<bool>& propagate_down, \ const std::vector<Blob<float>*>& bottom); \ template void classname<double>::Backward_gpu( \ const std::vector<Blob<double>*>& top, \ const std::vector<bool>& propagate_down, \ const std::vector<Blob<double>*>& bottom) #define INSTANTIATE_LAYER_GPU_FUNCS(classname) \ INSTANTIATE_LAYER_GPU_FORWARD(classname); \ INSTANTIATE_LAYER_GPU_BACKWARD(classname) caffe中定义的都是函数模板，是不会参与编译的，所以只有把函数实例化(INSTANTIATE)，编译器才会编译函数模板。类似的，我们在sigmoid_layer.cpp 文件中，代码最后的 INSTANTIATE_CLASS(SigmoidLayer); 也是同样的道理，将模板类实例化。 //------common.hpp #define INSTANTIATE_CLASS(classname) \ char gInstantiationGuard##classname; \ template class classname<float>; \ template class classname<double> reference [pdf] GPU Technology conference----CUDA C [pdf] CUDA范例精解通用GPU编程 caffe CUDA 相关宏定义 under-the-hood-caffe sigmoid_layer.cu caffe 中的一些编程规范
-
一分钟实现python安装包开发 1. 实现步骤： 创建一个setup.py文件。这个文件是Python安装包的核心，用于定义包的元数据、依赖关系和安装过程 使用setuptools、 wheel构建安装包 2. 举例：以实现函数计时功能为例 创建一个名为timer_decorator的Python包，它提供了一个计时器装饰器，用于测量函数的运行时间。 创建一个名为timer_decorator的目录。 在timer_decorator目录中创建一个名为__init__.py的文件，这将使其成为一个Python包。在__init__.py文件中，编写计时器装饰器的代码： import time def timer_decorator(func): def wrapper(*args, **kwargs): start_time = time.time() result = func(*args, **kwargs) end_time = time.time() print(f"{func.__name__} took {end_time - start_time:.2f} seconds to run.") return result return wrapper 创建一个setup.py文件，如下所示： from setuptools import setup setup( name='timer_decorator', version='0.1', py_modules=['timer_decorator'], install_requires=[ # 该项目没有依赖项 ], entry_points={ 'console_scripts': [ # 该项目没有可执行脚本 ], }, ) 基于setup.py创建whl安装文件 python setup.py timer_decorator 使用方法： from timer_decorator import timer_decorator @timer_decorator def my_function(): # Your code here
-
-
-
gtest in caffe 为了验证自己编写层的正确性，我们通过写xx_layer_test.cpp中测试层的前向和反向操作。caffe中运用Google C++ Testing Framework 来进行测试。 使用gtest(Google Test)使得程序的主体与测试独立开。使用gtest时，我们需要编写断言(assertion)，判断条件是否成立。Google Test中的断言类似于函数调用，例如ASSERT_EQ(val1,val2) 判断两个数是否相等。gtest中的宏，我们只要定义即可，不用显示地调用，gtest内部通过RUN_ALL_TESTS()为我们隐式地调用了这些测试。 TEST宏 以测试n!序列(1,2!,3!,...,n!)为例，介绍 TEST宏的用法 int Factorial(int n); // Returns the factorial of n // Tests factorial of 0. TEST(FactorialTest, HandlesZeroInput) { EXPECT_EQ(1, Factorial(0)); } // Tests factorial of positive numbers. TEST(FactorialTest, HandlesPositiveInput) { EXPECT_EQ(1, Factorial(1)); EXPECT_EQ(2, Factorial(2)); EXPECT_EQ(6, Factorial(3)); EXPECT_EQ(40320, Factorial(8)); } TEST宏的第一个参数相同，表明它们属于同一组测试，第二个参数表明具体的测试实例(处理0输入，处理正数输入)，宏的内部为需要测试的C++语句。 TEST_F宏 如果想要在不同的测试的case中访问通过一个变量或对象，我们可以定义一个测试类，将这些变量或对象定义成测试类中的成员变量。这个测试类，gtest中把它叫做Test Fixtures，并且gtest已经实现了它的父类::testing::Test, 我们只需要从该父类继承，便可节省许多代码量。 以对队列测试为例： template <typename E> // E is the element type. class Queue { public: Queue(); void Enqueue(const E& element); E* Dequeue(); // Returns NULL if the queue is empty. size_t size() const; }; class QueueTest : public ::testing::Test { protected: virtual void SetUp() { q1_.Enqueue(1); q2_.Enqueue(2); q2_.Enqueue(3); } // virtual void TearDown() {} Queue<int> q0_; Queue<int> q1_; Queue<int> q2_; }; TEST_F(QueueTest, IsEmptyInitially) { EXPECT_EQ(0, q0_.size()); } TEST_F(QueueTest, DequeueWorks) { int* n = q0_.Dequeue(); EXPECT_EQ(NULL, n); n = q1_.Dequeue(); ASSERT_TRUE(n != NULL); EXPECT_EQ(1, *n); EXPECT_EQ(0, q1_.size()); delete n; n = q2_.Dequeue(); ASSERT_TRUE(n != NULL); EXPECT_EQ(2, *n); EXPECT_EQ(1, q2_.size()); delete n; } TEST_F与TEST 使用的方法类似，不同之处在于，TEST_ F的第一个参数必须是类名。 TYPED_TEST 宏 这个宏与C++中的template类似，即我们希望利用相同的算法流程处理不同类型的变量。废话不多说，直接上例子。 template <typename T> class FooTest : public ::testing::Test { public: ... typedef std::list<T> List; static T shared_; T value_; }; typedef ::testing::Types<char, int, unsigned int> MyTypes; TYPED_TEST_CASE(FooTest, MyTypes); TYPED_TEST(FooTest, HasPropertyA) { ... } TYPED_TEST(FooTest, HasPropertyB) { ... } 首先，与TEST_F一样，我们首先从::testing::Test 中继承，注意到我们typedef了一个类型的列表为MyTypes, 并且调用TYPED_TEST_CASE 宏告诉gtest 我们需要测试这个列表中所有的类型。 gtest的调用 同样，以一个实例来介绍，gtest在cpp文件中如何调用测试 /* * gtest_main.cpp * * Created on: 23 Oct, 2016 * Author: lab-xiong.jiangfeng */ #include "gtest/gtest.h" #include <cmath> double square_root(const double x){ if(x<0){ return -1; } return sqrt(x); } TEST(SquareRootTest,PositiveNos){ EXPECT_EQ(18.0,square_root(324.0)); EXPECT_EQ(25.4,square_root(645.16)); EXPECT_EQ(50.332,square_root(2533.310224)); } TEST(SquareRootTest,ZeroAndNegtiveNos){ ASSERT_EQ(0.0,square_root(0.0)); ASSERT_EQ(-1,square_root(-22.0)); } int main(int argc,char **argv){ ::testing::InitGoogleTest(&argc , argv); //Note that RUN_ALL_TEST automatically detects and runs all the tests define using TEST macro return RUN_ALL_TESTS(); } main函数以上的内容我们都已经见过了，在main函数中，我们看到两个新的函数，InitGoogleTest 和RUN_ALL_TESTS 。顾名思义，InitGoogleTest 从命令行中解析参数并初始化。RUN_ALL_TESTS 自动检测我们定义的TEST 、TEST_F 等宏，然后测试所有的case。 gtest的基础部分就这么多，更多高级的用法可以参考googletest/AdvancedGuide.md test_scale_layer 接下来以scale_layer为例，进一步理解caffe中的测试环节。 让我们一步一步分析test_scale_laye_.cpp的组成，首先包含一些必要的头文件 #include <algorithm> #include <vector> #include "gtest/gtest.h" #include "caffe/blob.hpp" #include "caffe/common.hpp" #include "caffe/filler.hpp" #include "caffe/layers/scale_layer.hpp" #include "caffe/test/test_caffe_main.hpp" #include "caffe/test/test_gradient_check_util.hpp" 这些头文件我们已经比较熟悉了，接下来就是要测试的类的定义了， template <typename TypeParam> class ScaleLayerTest : public MultiDeviceTest<TypeParam> { typedef typename TypeParam::Dtype Dtype; 乍一看，MultiDeviceTest是什么鬼。。原来它是继承自::testing::Test 的一个类,它的作用是把Caffe::set_mode() 封装到这个类的构造函数中,实现不同Device下的测试。 TYPED_TEST_CASE(ScaleLayerTest, TestDtypesAndDevices); TYPED_TEST_CASE是不是看起来很熟悉，没错，这就是这就是上面我们提到的TYPED_TEST的用法，为了只用一个函数测试float 和double类型（在CPU和GPU下），所以TestDtypesAndDevices 自然是要测试的类型列表。TestDtypesAndDevices的定义在在test_caffe_main.hpp 中， typedef ::testing::Types<CPUDevice<float>, CPUDevice<double>, GPUDevice<float>, GPUDevice<double> > TestDtypesAndDevices; template <typename TypeParam> struct CPUDevice { typedef TypeParam Dtype; static const Caffe::Brew device = Caffe::CPU; }; template <typename TypeParam> struct GPUDevice { typedef TypeParam Dtype; static const Caffe::Brew device = Caffe::GPU; }; 再接下来就是ScaleLayerTest的各种暴力测试，主要就是一些前向后向操作，具体内容，就自己看代码test_scale_layer.cpp慢慢消化吧。 TYPED_TEST(ScaleLayerTest, TestForwardEltwise) TYPED_TEST(ScaleLayerTest, TestForwardEltwiseInPlace) TYPED_TEST(ScaleLayerTest, TestBackwardEltwiseInPlace) TYPED_TEST(ScaleLayerTest, TestForwardEltwiseWithParam) TYPED_TEST(ScaleLayerTest, TestForwardBroadcastBegin) TYPED_TEST(ScaleLayerTest, TestForwardBroadcastMiddle) TYPED_TEST(ScaleLayerTest, TestForwardBroadcastMiddleInPlace) TYPED_TEST(ScaleLayerTest, TestBackwardBroadcastMiddleInPlace) TYPED_TEST(ScaleLayerTest, TestForwardBroadcastMiddleWithParam) TYPED_TEST(ScaleLayerTest, TestForwardBroadcastMiddleWithParamAndBias) TYPED_TEST(ScaleLayerTest, TestForwardBroadcastEnd) TYPED_TEST(ScaleLayerTest, TestForwardScale) TYPED_TEST(ScaleLayerTest, TestForwardScaleAxis2) TYPED_TEST(ScaleLayerTest, TestGradientEltwise) TYPED_TEST(ScaleLayerTest, TestGradientEltwiseWithParam) TYPED_TEST(ScaleLayerTest, TestGradientBroadcastBegin) TYPED_TEST(ScaleLayerTest, TestGradientBroadcastMiddle) TYPED_TEST(ScaleLayerTest, TestGradientBroadcastMiddleWithParam) TYPED_TEST(ScaleLayerTest, TestGradientBroadcastEnd) TYPED_TEST(ScaleLayerTest, TestGradientScale) TYPED_TEST(ScaleLayerTest, TestGradientScaleAndBias) TYPED_TEST(ScaleLayerTest, TestGradientScaleAxis2) THE END ~.~
-
基础知识整理 深度学习(计算机视觉) 分类(网络结构发展过程) AlexNet --> VGG/GoogleNet --> ResNet/DenseNet BatchNorm / LayerNorm / InstanceNorm / GroupNorm 归一化能够加速网络收敛，归一化后梯度更稳定，能够采用更大的学习率 四种归一化的方式不同之处在于归一化所采用的统计量（均值，方差）不同 BatchNorm使用NHW的统计量$R^{C}$ LayerNorm使用CHW的统计量$R^{N}$ InstanceNorm使用HW的统计量$R^{N * C}$ GroupNorm使用GHW的统计量$R^{N * C/G}$ BatchNorm 在训练过程中通过滑动平均进行统计，增加了训练的随机性，而其它几种归一化的方式都是由单个样本得到的统计量，可能导致泛化能力比BatchNorm弱 轻量化网络 squeezeNet shuffleNet MobileNet 胶囊网络 几种特殊的卷积 空洞卷积 转置卷积 可分离卷积 模型量化/压缩
-
