1. 前言

梯度下降法的基本原理是，通过对目标函数做泰勒展开，当变量的运动方向与梯度方向相同，目标函数值增长最快；负梯度方向，目标函数值减小最快。这里主要讨论将目标函数做一阶泰勒展开，也就是一阶梯度优化方法。利用二阶泰勒展开,即牛顿法需要计算Hessian矩阵的逆，计算量大，在深度学习中并不常用。BGD(Batch Gradient Decent)利用整个训练集计算梯度，优化速度慢，需要一次将所有数据加载进内存不适用于在线学习，因此，在神经网络的优化中常采用mini-batch SGD(Stochastic Gradient Descent)进行优化。SGD主要存在以下两个问题：

• 难以确定学习率，并且不同的参数需要不同大小的学习。SGD比BGD收敛更快，但在最优解附近可能调整过大，导致在最优点附近震荡，因此基于SGD的算法，随着迭代的进行，不断减小学习率来解决这个问题。例如Caffe中有poly,inv,step等策略来调整学习率
• 鞍点(各个方向，梯度为0)的存在使得基于梯度的优化方法，难以逃离鞍点

2. 主要内容

• SGD+Momentum
• NAG
• AdaGrad
• RMSProp
• AdaDelta
• Adam

这里主要以尽可能简单的语言总结各个算法的内容，具体细节参考文末链接

3. 各个算法的特点

SGD+Momentum

动量统计了参数梯度的历史信息，参数当前的更新量不只与当前的梯度值有关，还与历史的累计梯度(动量项)有关，即指数衰减的移动平均。这样可以减少单次更新中，梯度估计不准确(方差大)带来的坏影响，动量的引入相当于对梯度进行平滑滤波

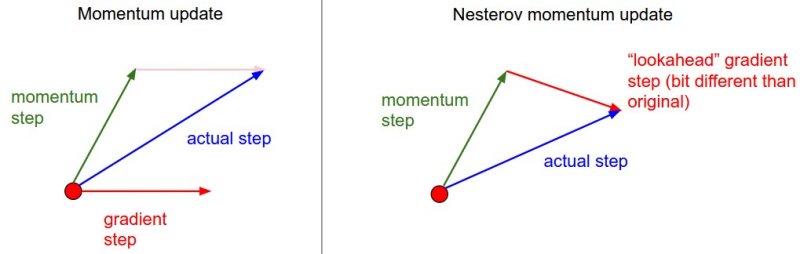
Nesterov Accelerated Gradient

Nesterov对梯度进行修正，先沿着原来的动量方向走一步，再求梯度。然后将该修正的负梯度值与历史动量叠加，得到当前的参数更新方向，如下图所示(右)

AdaGrad

AdaGrad属于自适应的一阶梯度优化算法，AdaGrad对学习率除以梯度平方累积和的开根号，这样使得梯度大的参数的学习率小，而梯度小的或者更新频率小的参数的学习率大(因此，更AdaGrad适用于稀疏数据)。
AdaGrad存在的一个最大的问题就是，随着学习的过程，梯度平方和不断增大，使得学习率不断减小，导致学习过早停止，后续的一些算法如RMSProp和AdaDelta就是为了解决这一问题而提出的。

AdaDelta

AdaDelta利用参数变化量滑动平均的开根号（指数衰减）和梯度平方滑动平均开根号的比值去近似二阶导数。使得AdaDelta去可以省去全局学习率的定义，同时也解决了AdaGrad中训练过早停止的问题。

RMSProp

RMSProp对比于AdaGrad的改进在于，RMSProp 通过滑动平均去统计梯度的平方，利用该滑动平均的值替换AdaGrad中梯度平方的累加和

Adam (Adaptive Moment Estimation )

Adam是RMSProp的改进版本，Adam在RMSProp的基础上，对梯度的估计加入了动量，另外对两个滑动平均(梯度和梯度的平方)进行无偏估计修正。例如对于梯度$g\_t$, 得到的平均值为 $v\_t = \alpha v\_{t-1}+(1-\alpha)g \_t$。在初始训练阶段，动量的初始值$v\_0=0$，那么第一项在初始阶段都偏小，因此Adam对平均值乘以$\frac{1}{1-\alpha^t}$ 进行无偏修正(e.g. 当$\alpha=0.9$,$t=1$时，修正的$\hat{v\_1} = \frac{1}{1-\alpha} * v\_1 = g\_1$)

reference

• CS231N Neural Network
• Hinton: Overview of mini-batch gradient descent
• An overview of gradient descent optimization algorithms
• Adam那么棒，为什么还对SGD念念不忘 (1)——一个框架看懂优化算法
• Adam那么棒，为什么还对SGD念念不忘 (2)—— Adam的两宗罪
• Adam那么棒，为什么还对SGD念念不忘 (3)—— 优化算法的选择与使用策略